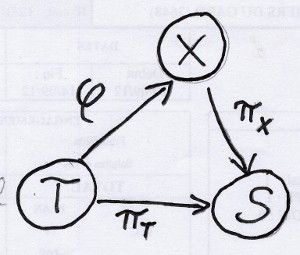
S : domaine de constantes, corps de définition
à valeur dans le "domaine universel" T
correspond au morphisme φ de T dans X
tel que
Schéma = mécanisme interne, martice, qui engendre les points de l'espace.
L’idée même de schéma est d’une simplicité enfantine – si simple, si humble, que personne avant moi n’avait songé à se pencher si bas. Si “bébête” même, pour tout dire, que pendant des années encore et en dépit de l’évidence, pour beaucoup de mes savants collègues, ça faisait vraiment “pas sérieux”! Il m’a fallu d’ailleurs des mois de travail serré et solitaire, pour me convaincre dans mon coin que “ ça marchait” bel et bien – que le nouveau langage, tellement bébête, que j’avais l’incorrigible naïveté de m’obstiner à vouloir tester, était bel et bien adéquat pour saisir, dans une lumière et avec une finesse nouvelles, et dans un cadre commun désormais, certaines des toutes premières intuitions géométriques attachées aux précédentes “géométries de caractéristique p”. (Récoltes et semailles, cité par Scharlau)
Les schémas sont une manière de coder les systèmes d'équations et les transformations qu'on peut leur faire subir.Une solution du "système d'équations" X avec le "domaine de constantes" S T : domaine universel
T : domaine universel
S : domaine de constantes, corps de définition
à valeur dans le "domaine universel" T
correspond au morphisme φ de T dans X
tel queπT = πX • φ
Schéma = mécanisme interne, martice, qui engendre les points de l'espace.
φ est un T-point du S-schéma X et ceci quelque soit le S-schémaUn pays dont on ne connaîtrait que le nom (Grothendieck et les « motifs »)
La géométrie algébrique est le domaine où l’on étudie le lieu des solutions d’ensembles d’équations polynomiales en combinant les propriétés algébriques des anneaux de polynômes avec les propriétés géométriques de ce lieu, connu sous le nom de variété. Traditionnellement, il s’agissait des solutions complexes de polynômes à coefficients complexes mais juste avant le travail de Grothendieck, André Weil et Oscar Zariski avaient compris que l’on gagnait considérablement en ampleur et profondeur en considérant des solutions et des polynômes sur des corps arbitraires, par exemple sur des corps finis ou sur des corps de nombres algébriques.Les fondements adéquats de cette vision élargie de la géométrie algébrique étaient néanmoins peu clairs et c’est là que Grothendieck fit sa première innovation, immensément significative : il a inventé une classe de structures géométriques généralisant les variétés qu’il appela des schémas. Dit de la manière la plus simple, il proposa d’associer à tout anneau commutatif (n’importe quel ensemble d’objets pour lesquels l’addition, la soustraction et une multiplication commutative sont définies, comme l’ensemble des entiers ou l’ensemble des polynômes en les variables
x,y,z à coefficients complexes) un objet géométrique, appelé soit le Spec de l’anneau (raccourci de spectre) soit son schéma affine, et de recoller de tels objets entre eux pour former un schéma. L’anneau est pensé comme ensemble de fonctions sur son schéma affine.Pour illustrer à quel point cette idée a été révolutionnaire, un anneau peut être fabriqué en partant d’un corps, disons celui des nombres réels, et en rajoutant une quantité
ϵ qui satisfaitϵ2=0 . Pensez àϵ de la manière suivante : vos instruments peuvent vous permettre de mesurer une petite quantité telle queϵ=0,001 mais alorsϵ2=0,000001 pourrait être trop petit pour être mesuré, donc il n’y a pas de mal à dire qu’il est égal à zéro. Les nombres dans cet anneau sont de la formea+b⋅ϵ aveca etb réels. L’objet géométrique auquel correspond cet anneau est un vecteur infiniment petit, un point qui peut bouger de manière infinitésimale, mais seulement au premier ordre. Grothendieck revint à Leibniz, en concevant ainsi les infinitésimaux comme des objets qui peuvent être manipulés. Une idée semblable a récemment été utilisée en physique, pour les supercordes.Pour relier les schémas à la théorie des nombres, on prend l’anneau des entiers. Le Spec correspondant a un point pour chaque nombre premier, en lequel les fonctions prennent des valeurs dans le corps fini des entiers modulo
p , et un point classique en lequel les fonctions prennent des valeurs rationnelles, et qui est plus « gros », car il a tous les autres points dans son adhérence.Dès que cette construction devint familière, peu nombreux furent ceux qui doutèrent qu’il avait trouvé les fondements corrects pour la géométrie algébrique. Elle est à présent universellement acceptée.
Peut-on expliquer les schémas aux biologistes ?
Pour la Science N° 467 septembre 2016 : Les maths de Grothendieck - L'héritage fertile d'un génie