C’est le thème du topos qui est ce “lit”, ou cette “rivière profonde” où viennent s’épouser la géométrie et l’algèbre, la topologie et l’arithmétique, la logique mathématique et la théorie des catégories, le monde du continu et celui des structures “discontinues” ou “discrètes”. Il est ce que j’ai conçu de plus vaste, pour saisir avec finesse, par un même langage riche en résonances géométriques, une “essence” commune à des situations des plus éloignées les unes des autres provenant de telle région ou de telle autre du vaste univers des choses mathématiques”. Alexandre Grothendieck, Récoltes et semailles, cité par Caramello
Voici donc l’idée nouvelle. Son apparition peut être vue comme une conséquence de cette observation, quasiment enfantine à vrai dire, que ce qui compte vraiment dans un espace topologique, ce ne sont nullement ses “points” ou ses sous-ensembles de points, et les relations de proximité etc. entre ceux-ci, mais que ce sont les faisceaux sur cet espace, et la catégorie qu’ils forment.
Je n’ai fait, en somme, que mener vers sa conséquence ultime l’idée initiale de Leray – et ceci fait, franchir le pas. Alexandre Grothendieck, Récoltes et semailles, cité par Scharlau
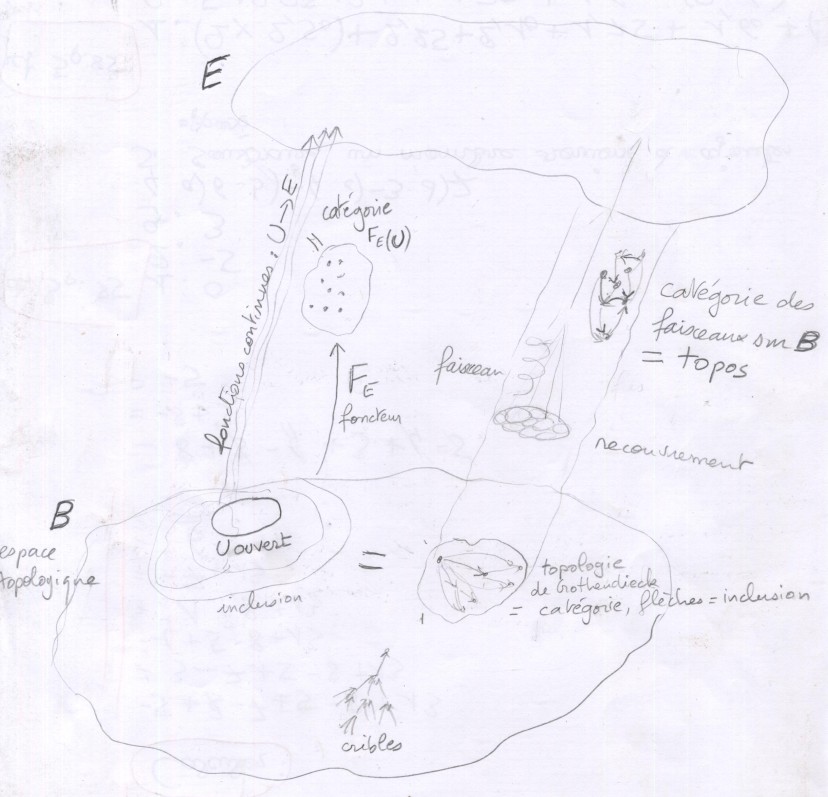
L'observation fondamentale de Grothendieck est le fait qu'essentiellement quand on considère les faisceaux sur un espace topologique, il y a deux structures qui sont fondamentales dans cette définition :Soyons clairs : je n'ai pas vraiment compris ce qu'est un topos. Mais à force de chercher, j'ai fini par comprendre que c'est vraiment important, et j'ai peut-être un peu compris comment ça marche.Ce sont ces ingrédients qui sont essentiels et suffisants pour la définition du topos. Interview d'Olivia Caramello par Stéphane Dugowson et Anatole Khelif a l'IHES - 27'20''
- la catégorie des ouverts de l'espace, une catégorie simple, une catégorie pré-ordonnée dans laquelle les flèches sont simplement les inclusions
- et la notion de recouvrement d'un ouvert par une famille de sous-ouverts.
Recouvrement
On se place dans un espace habituel, par exemple le plan, où on peut définir la notion d'ouvert (ensemble qui ne contient pas ses propres limites).On appelle
B cet espace.
Par exemple,
] 0, 1 [, l'ensemble des nombres réels compris entre 0 et 1, strictement > 0 et < 1.
Si on a un ouvert
U de B,
un recouvrement de
est une famille
telle que la réunion des
U
est une famille
Ui d'ouverts de B
telle que la réunion des
Ui donne U
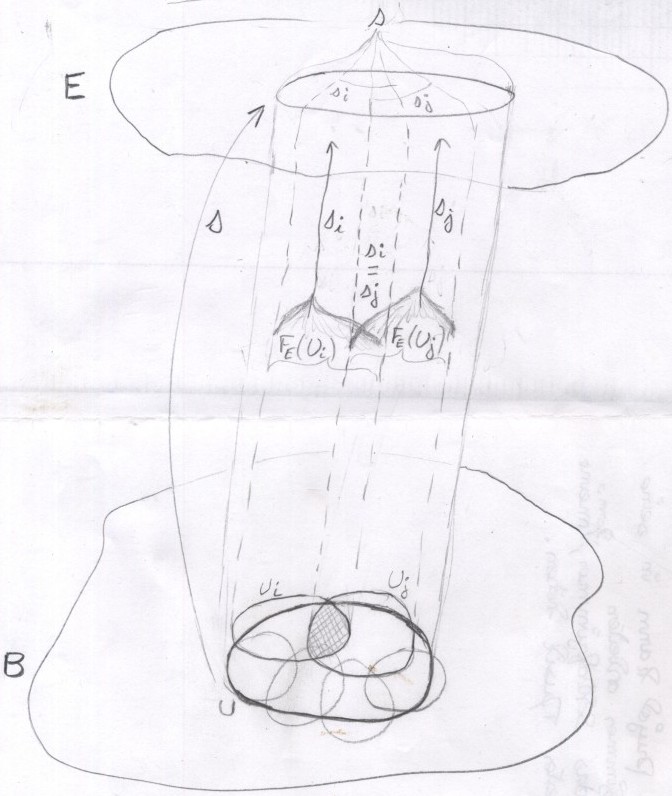
Faisceaux
On a un deuxième espace, que l'on nommeE
On note
FE(U) l'ensemble des applications continues de B dans E.
Application continue : si on fait subir une "transformation continue" à
U (si U varie de manière infinitésimale), alors FE(U) varie aussi de manière continue.
Topos