Plancher de la yourte - Plans

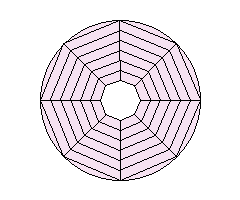Afin d’avoir une yourte démontable et transportable, j’ai opté pour un plancher “en étoile” (ou en camembert).
On divise le cercle en n parties égales. Pour ma part, j’ai choisi n = 8 (voir plus bas pour la justification de ce choix).
J’ai choisi de laisser un trou central en me disant que c’est plus facile à réaliser car ça laisse plus de marge par rapport aux erreurs de construction : je sentais mal l’assemblage au centre avec des pointes (sans parler de la découpe des chevrons). Et je trouvais intéressant d’avoir un accès à la “cave” de la yourte, si le plancher est posé sur pilotis.

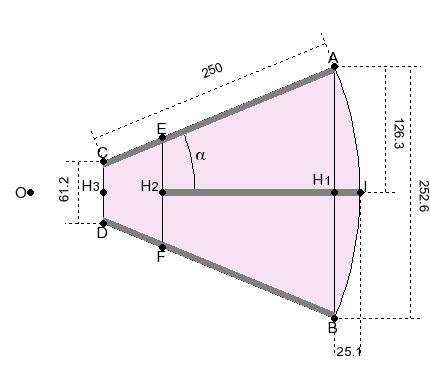
Plan d’un élément de plancher

On connaît :

- R, le rayon de la yourte

On définit :

- n, le nombre d’éléments de plancher
- r1, le diamètre du trou central
- pm, la portée maximale des planches
Pour la réalisation, j'ai pris des planches en châtaigner de 30 mm d'épaisseur et des chevrons de 6 x 8 cm (en douglas).
Les planches sont vissées sur les chevrons parallèlement à CD, EF ou AB, ce qui assure la forme et la rigidité du plancher.
Il y a deux chevrons sur les bords (AC et BD sur le schéma) ; un chevron supplémentaire (H₂I) sert à limiter la portée des planches.
Le choix de n a été guidé par deux éléments :
- la portée maximale des planches (AH₁ ou H₁B).
- la valeur du dépassement H₁I.
J'ai regardé ce que ça donnait pour différentes valeurs de n.
Avec un rayon de 3 m 30 et n = 8, on a : AB = 2 m 52 et H₁I = 25 cm.
La portée maximale est de AB / 2 - 1,5 e (e étant l'épaisseur des chevrons, ici 6 cm),
ce qui donne une portée maximale de 1 m 15.
D'après les infos que j'ai pu glaner, c'est un peu trop, mais j'ai quand même conservé une division par 8, car cette portée excessive ne concerne qu'une ou deux planches à chaque fois (celles qui sont près de AB), et j'ai cherché à faire le moins d'éléments de plancher possible. Ce choix implique de faire attention de ne pas mettre de choses lourdes aux endroits de fragilité ; en cas de problème, on peut toujours visser des planches dessous pour renforcer. Pour l'instant, avec des planches de 3 cm d'épaisseur on n'a pas eu de problème.
Pour la portée, il faut aussi se soucier de EF ; il suffit de choisir correctement la position de H₂ pour ne pas être embêté (calculé par programme).

Valeurs correspondent à la yourte que j'ai fabriqué :

OC = 80 cm CE = 63.7 cm EA = 186.3 cm CA = 250 cm

CD = 61.2 cm EF = 110 cm AB = 252.6 cm

OH3 = 73.9 cm H3H2 = 58.9 cm H2H1 = 172.1 cm H2I = 197.2 cm H1I = 25.1 cm

Le plan et le tableau de valeurs ont été générés par programme (yourte_plancher.php), voir la page Programme pour une yourte

Formules principales

• α = π / n
• OC = R1
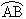• = 2 R α
• AB = 2 R sin α
• OH₁ = R cos α
• H₁I = R (1 - cos α )
• OH₂ = R1 cos α

(voir le programme pour les autres formules)

Le chevron H₂I sert à supporter les planches d'une longueur supérieure à la portée max.
Il faut donc déterminer H₂ tel que EF = pm (portée max).
Par Thalès : OE / OA = EF / AB, donc OE = R x EF / AB
J'ai pris EF = 1 m 10 (ce qui fait une portée de 98 cm en enlevant l'épaisseur des chevrons).

Tracé de l'arrondi

En vissant les planches parallèles, on comble la surface ABCD ; reste à compléter avec la partie arrondie ; yourte_plancher_arrondi.php m'a servi à obtenir les mesures pour découper l'arrondi du plancher.
Ce programme génère soit un schéma, soit un tableau avec les mesures.
Les mesures sont utilisées 2 fois pour chaque élément de plancher ; le 0 correspond au milieu du plancher
Voila les mesures obtenues pour notre yourte :

Schéma

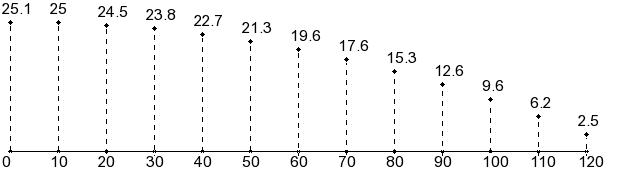
Tableau de mesures

x	0	10	20	30	40	50	60	70	80	90	100	110	120
y	25.1	25	24.5	23.8	22.7	21.3	19.6	17.6	15.3	12.6	9.6	6.2	2.5

Détail des calculs

Le but est de pouvoir calculer la distance H_iM_i en fonction de HH_i
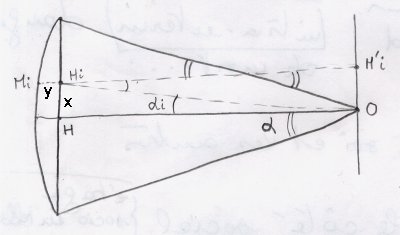
On note : x = HH_i et y = H_iM_i
Pour ce programme, les données de départ sont :
- R, rayon de la yourte
- n, nombre de divisions du cercle
Et on a toujours : α = π / n

Calcul de x = HH_i :
on a : HH_i = OH'_i, donc x = R sin α_i

Calcul de y = M_iH_i :
On a : M_iH'_i = R cos α_i
et : H_iH'_i = HO = R cos α
Comme M_iH_i = M_iH'_i - H_iH'_i, on obtient : y = R(cos α_i - cos α)

Algorithme :
On va prendre x tous les δ centimètres (il faut choisir δ, j'ai pris 10 cm).
Pour chaque x que l'on prend, on calcule α_i : α_i = arcsin (x / R) ; une fois qu'on connaît α_i, on peut calculer y.