Treillis de la yourte - Plans

Le treillis sert d'ossature au mur de la yourte. Ce sont des croisillons de tasseaux attachés à leurs intersections par des ficelles ou lacets de cuir (les tasseaux sont percés, et la ficelle passe dans le trou ; tous les noeuds que j'ai vus sont bien serrés). Après avoir vu quelques yourtes et discuté de la question, j'ai retenu de le faire avec des tasseaux 4 x 3 cm, en douglas.

Toutes les yourtes que j'ai pu voir ont un treillis qui repose sur le plancher, mais j'ai entendu parler d'une yourte dont le treillis repose sur le sol, et qui utilise le plancher pour prendre la forme de cercle.
J'ai posé le treillis en bordure de plancher ; le diamètre extérieur du treillis est celui du plancher (6m60)

Quelques considérations :
- Il faut fixer le treillis au plancher, sinon la yourte peut vriller : le treillis se déplace et la couronne se met à pencher.
- Les perches se fixent sur le treillis, donc chaque perche repose sur le haut d'un losange, donc le nombre de losanges horizontaux est égal aux nombre de perches.
- Tous les treillis que j'ai vus ont un nombre de losanges verticaux multiples de 0,5 (3 ou 3,5 ou 4 etc.). En fait, ce n'est pas obligatoire ; en haut, les perches doivent reposer sur une intersection, mais en bas, avoir un multiple de 0,5 permet de faire reposer le treillis au niveau d'une intersection. C'est peut-être plus solide.
- Il faut demander des tasseaux sans noeud, car ça fragilise le bois.

On connaît :

- D, le diamètre de la yourte ;
- h, la hauteur de la yourte ;
- np, le nombre de perches de la yourte ;

On définit :

- etas, épaisseur des tasseaux

Périmètres

Le treillis se cale sur le bord du plancher ; le périmètre que doit couvrir le treillis n'est pas égal au périmètre de la yourte, mais correspond à un rayon de R - etas.
On définit donc pdt, le périmètre que le treillis doit couvrir (pdt pour "périmètre du treillis").

On a : pdt = 2 π (R - etas)

Il faut ensuite déterminer quelle partie du périmètre le treillis va couvrir ; enlever à pdt la longueur prise par les portes et fenêtres.
On définit donc :
- pst : périmètre sans treillis
- pat : périmètre avec treillis
Il faut choisir pst

On a : pat + pst = pdt

Losanges

Pour caractériser les losanges, on doit définir un certain nombre de variables :
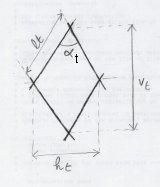
- lt, ht, vt, αt (voir figure) ;
- nt, le nombre de losanges verticaux.
On doit fixer nt, et toutes les autres variables s'en déduisent.

La hauteur à considérer pour calculer la taille des losanges n'est pas exactement h, à cause de dépassements en haut et en bas.
On définit donc :
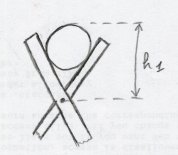
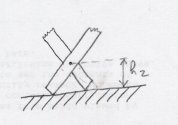
- h1 : dépassement en haut ;
- h2 : dépassement en bas ;
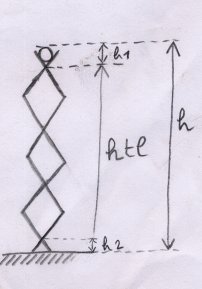
- htl : hauteur totale des losanges.

Figure 2 Figure 3

Figure 4

On a : htl = h - h1 - h2

J'ai choisi les hauteurs h1 et h2 un peu au pif, en vissant 2 bouts de bois pour simuler un morceau de treillis et en mesurant ce que ça donne. Une fois les calculs effectués, j'ai refait le montage avec la bonne valeur de αt, ce qui m'a permis de réévaluer h1 et h2.

Calculs :
Le nombre de perches est égal au nombre de losanges horizontaux, donc ht est imposé par pdt et np :

ht = pdt / np

On doit choisir nt, le nombre de losanges verticaux, ce qui permet de déduire vt :

htl = vt * nt, donc vt = htl / nt

On peut maintenant connaître lt et αt :

Par Pythagore,

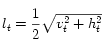
tg(αt / 2) = ht / vt, soit : αt = 2 arctan(ht / vt)

Construction

Sur la figure 5, il y a 3,5 losanges verticaux et chaque tasseau compte 7 longueurs de losanges.

La longueur d'un tasseau est : ltas = 2 * nt * lt + (h1 + h2) / cos(αt/2)

Position des trous

Le premier trou est à h1 / cos(αt / 2) ; les trous suivants sont distants de lt.

Assemblage

Sur la figure 5, on voit qu'il y a 7 intersections par ligne ; si on fait bouger les traits de fin verticaux, on voit qu'une rangée peut en contenir 6 ou 7. Une longueur donnée, l peut donc en contenir en gros ht/l.

ntas = 2 * pat / ht

Nombre de tasseaux à acheter : ntas = 2 * pat / ht

En vrac

On peut aussi s'amuser à calculer le nombre d'intesections (donc le nombre de noeuds à faire...).

ni = ntas * (2 * nt + 1)

Valeurs pour notre yourte

Tous ces calculs sont faits par programme, voir la page Programme pour une yourte.